Today, if we were to wander around the nation’s industrial facilities and laboratories, we would find electronic balances being used for everything from counting batches of resistors to adjusting the component ratio of epoxy mixtures. Many of these balances are suitable for the most demanding analytical work, while others are less precise but serve many
purposes well. In the following discussion the analytical balance is defined as an instrument with capacities ranging from 1 g to a few kilograms and with a precision of at least one part in 10s of maximum capacity. Many modern electronic balances have a precision of one part in 107 at full capacity, and the accuracy is usually comparable. The inspiration for the modern analytical balance came from a weighing method change suggested by Borda (1).
To overcome the difficulties of unequal arm lengths inherent with the two-pan, equal-arm balance, Borda suggested a method known as substitution weighing to be used in place of transposition weighing. In 1886 a balance was designed and built specifically for substitution weighing, although the modern one-pan substitution balance did not become commonplace until the 1950s. Although these balances are completely mechanical in operation, the optical readout system was usually assisted with a light bulb.

The Analytical Balance and the Mass

UnitBefore looking in detail at the electronic balances, it is worthwhile to consider how mass is determined from a balance weighing and to briefly look at the inner workings of a modern mechanical substitution balance. The reader should keep in mind that of the many forces the balance can respond to, we are only interested in the gravitational and buoyant forces and would like to exclude all others.

First, we must recognize that the balance reading is not the mass of the sample being weighed and therefore is not the desired result. The balance manufacturer has built the balance to indicate so-called apparent mass of the material being weighed. In essence, if the material being weighed has a density of 8.0 g/cm3 at 20 °C anc the air density is 0.0012 g/cm3, then and only then does the balance indicate the mass of the object being weighed.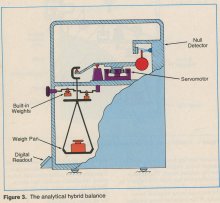 Obviously, these conditions are rarely met, and the balance reading must be corrected to get the desired mass (2).

The important point of the above discussion is that all analytical balances are calibrated by the manufacturers to indicate what is known as “apparent mass vs. 8.0 g/cm3.” In some instances the balance may actually contain a single weight or a set of weights, or a weight may be supplied separately by the balance manufacturer for calibration of the balance. It is from this initial calibration and subsequent recalibrations that the user is tied to the mass unit, directly for standard conditions and by computation for all other conditions.
For many years another apparent mass scale based on this principle had been in use. The basis of this scale was a brass weight whose density was specified to be 8.3909 g/cm3 at 20 °C with an air density of 0.0012 g/cm3. This scale is generally referred to as the “apparent mass vs. brass” scale.

Balance Principles

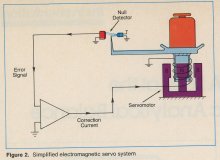
Today there are two dominant types of electronic balances in use — the hybrid and the electromagnetic force balance. The hybrid balance uses a mix of mechanical and electronically generated forces, whereas the electromagnetic force balance uses electronically generated forces entirely. A brief review of mechanical balance principles is worthwhile before the hybrid and electromagnetic force balances are discussed. In all cases, a null indicator is used to determine when the internal force balances the gravitational force on the sample.

The Mechanical Balance. The modern mechanical balance is a one-pan, two-knife balance with the applied gravitational force on the pan nearly counterbalanced by a fixed weight built into the balance beam. Any residual inequality of forces causes an angular displacement of the beam. Equilibrium is reestablished by adding or subtracting internal weights.

Figure 1 is a schematic of a typical one-pan mechanical balance. The balance readout is attained by summing the weight dial indications with a beam displacement indicator such as a projected optical scale. Whatever means are used to indicate the angular displacement of the balance beam, the balance is manufactured and calibrated to indicate the same
apparent mass scale as that of the built-in weight. The prominent features are the built-in weights (i.e., mass standards) and beam damping. However, of significance is the constant loading of the balance beam regardless of the sample weight on the pan. This feature provides a constant balance sensitivity; that is, the angular beam displacement in response to a small force change remains constant regardless of pan loading, a characteristic not found in equal-arm balances.